tenurepro
New member
Hi All,
I thought it would be fun to put this out there after some discussions on the leopard wrasse thread. Essentially; some folks claim that a certain group of fish never jump (because of personal experience of keeping a few fish) while others claim that the same group of fish are jumpers and are thus ultimately doomed to certain death in an open top tank. This little writeup shows how both view points can be reconciled with some simple math.
Ok, we hear a lot of general statements about certain fish being jumpers versus others that are not. But obviously, there are some individual specific tendencies (personality), species specific tendencies, genera specific tendencies, and all of this is modified by the tank environment (etc. size of tank, depth, interactions with other fish). I don't really think that fish are either jumpers or not jumpers... way too binary. For the simplicity of the model developed below, lets think of fish have a 'probability' of jumping for any given day; this probability depends on species (some species of fish/wrasse have higher probabilities of jumping than others) and tank environment / scape. We can probably all agree that most fish can in theory jump, so the probability of jumping is almost always a number that is greater than zero.
If the probability of jumping is greater than zero and substantially high. (say 10% a day), then it is inevitable that the fish will jump given enough time, and that a cover is absolutely needed to keep the fish alive in a tank.
Even if the probability of jumping is really low, say, 1 in 100,000 (0.001%) a day... it doesn't mean that the fish will never jump. Given enough time, rare events will occur (think of people winning the lottery, or getting struck by lighting... it happens, but it is rare). When we are dealing with such low probabilities, then it is totally conceivable to see how some reefers can keep the same species in an open top without them ever jumping, while others having them jump a few times... (just like some people win the lottery while most don't; you can't argue that just because you didn't' win the lottery, that nobody wins the lottery; also, you can't argue that if you win the lottery, than every one will win the lottery)...
So i decided to explore some models of fish jumping in an open top tank given a CONSTANT (assumption) daily probability of jumping. The constant assumption and the discrete nature of jumping (and dying) vs. not jumping (and living) make this problem very easy to model with the binomial distribution. if you were sick during math in high school, then the binomial is the little (n choose k) equation, where you predict the number of success or failures in N trials, assuming the probability of success or failure is constant. You can use the binomial to determine the probability of tossing a fair coin 20 times and getting only 5 tails for example.
In the context of fish jumping, we set the probability of success = daily probability of fish jumping, and ask how many times we observe 0 jumps over time... that gives us the probability of fish NOT jumping... 1- probability of fish NOT jumping is the same as the probability of fish jumping.
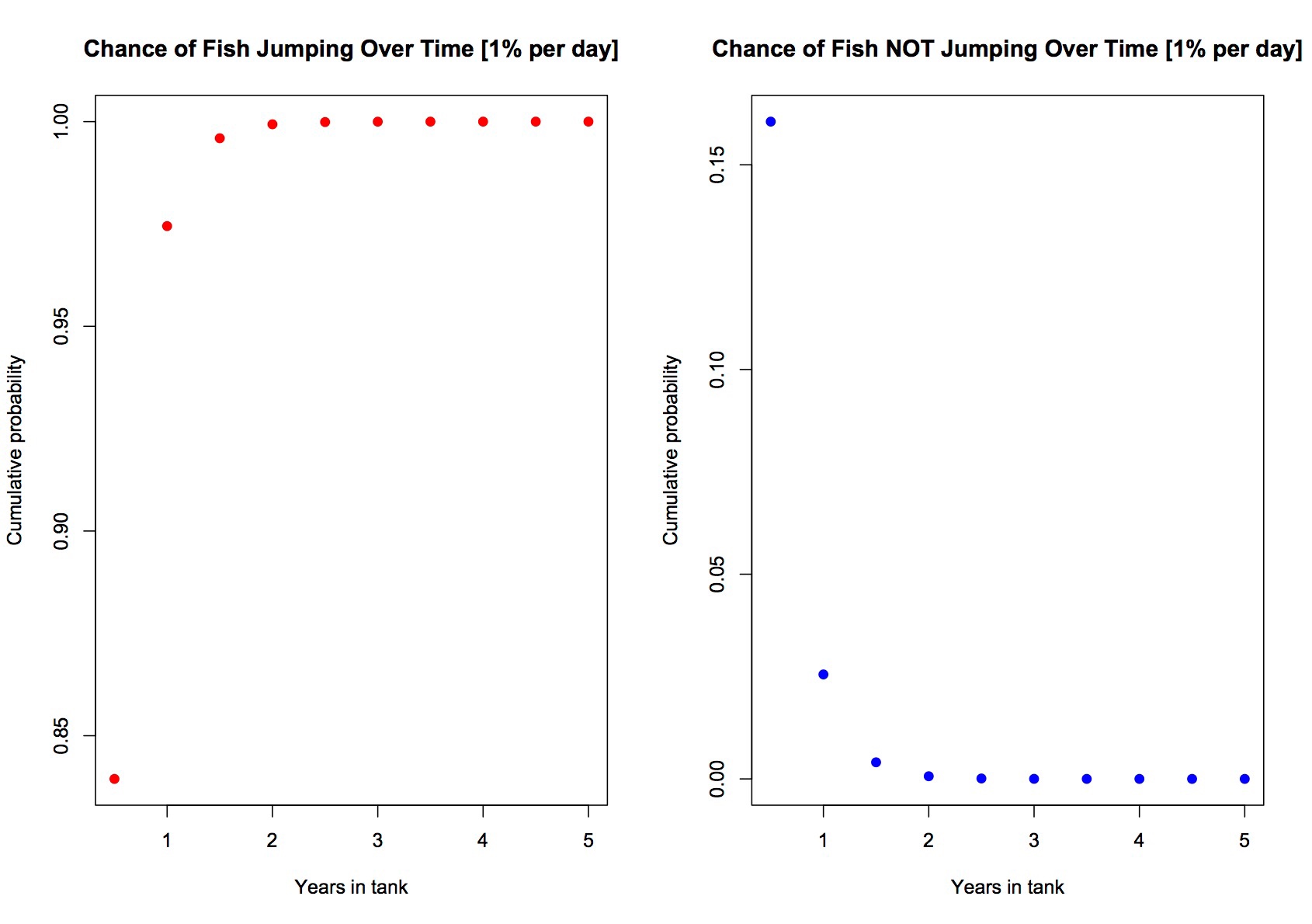
So here is the first model "“ assuming a fish has a 1% chance of jumping per day"¦ The probability that this fish would have jumped within the first year is close to 97.5%, The probability of this fish NOT jumping on you for a year is a measly ~2.5%... You NEED to get a cover if you want to keep this fish as the chance of keeping one in a tank with an open top for more than a few months are incredibly LOW.
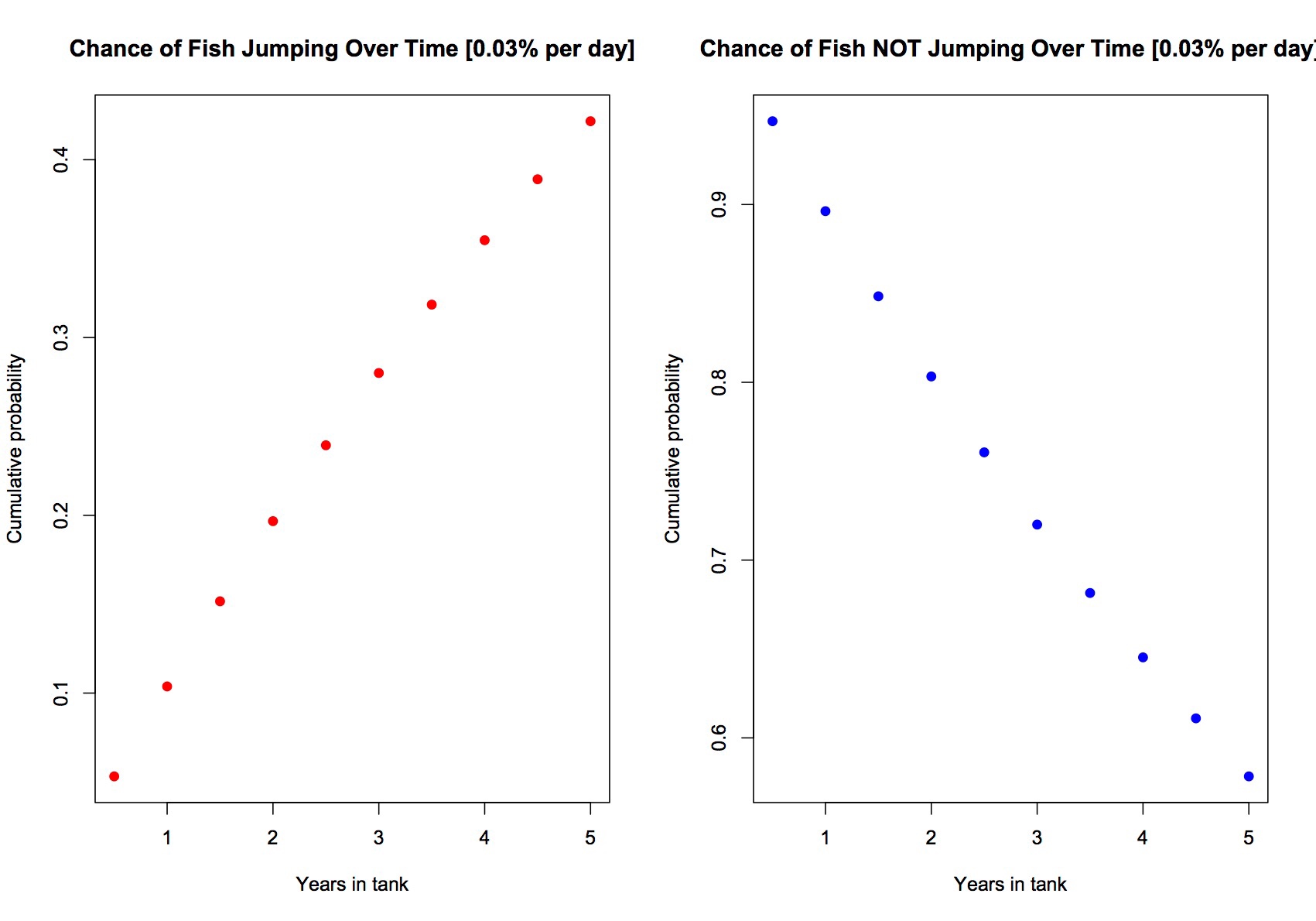
The second model has a daily probability of jumping at 3 in 10,000 (.03%); here we get into the grey zone. The chances of this fishing jumping by year one is about 10%, year 2 is about 20%, year 3 is about 30%, and year 5 is about 45%. The flip coin of this is you can almost certainly keep this fish alive in an open top tank (i.e. chance of fish NOT jumping) for a year, or two with only a small risk of it jumping). By 5 years though, it gets very dicey "¦ that is to say that half of the people that attempt this fish in an open top tank for 5 years will be successful while the others will not. This is where we tend to see a lot of debate between reefers; One will argue that I kept fish X for 5 years in an open top without it carpet surfing, so "œthey are not jumpers", while another will say, I tried fish X and it went carpet surfing, so "˜they are jumpers"; here is where the fallacy of observation bites us in the *** (with the binomial distribution laughing in the background).
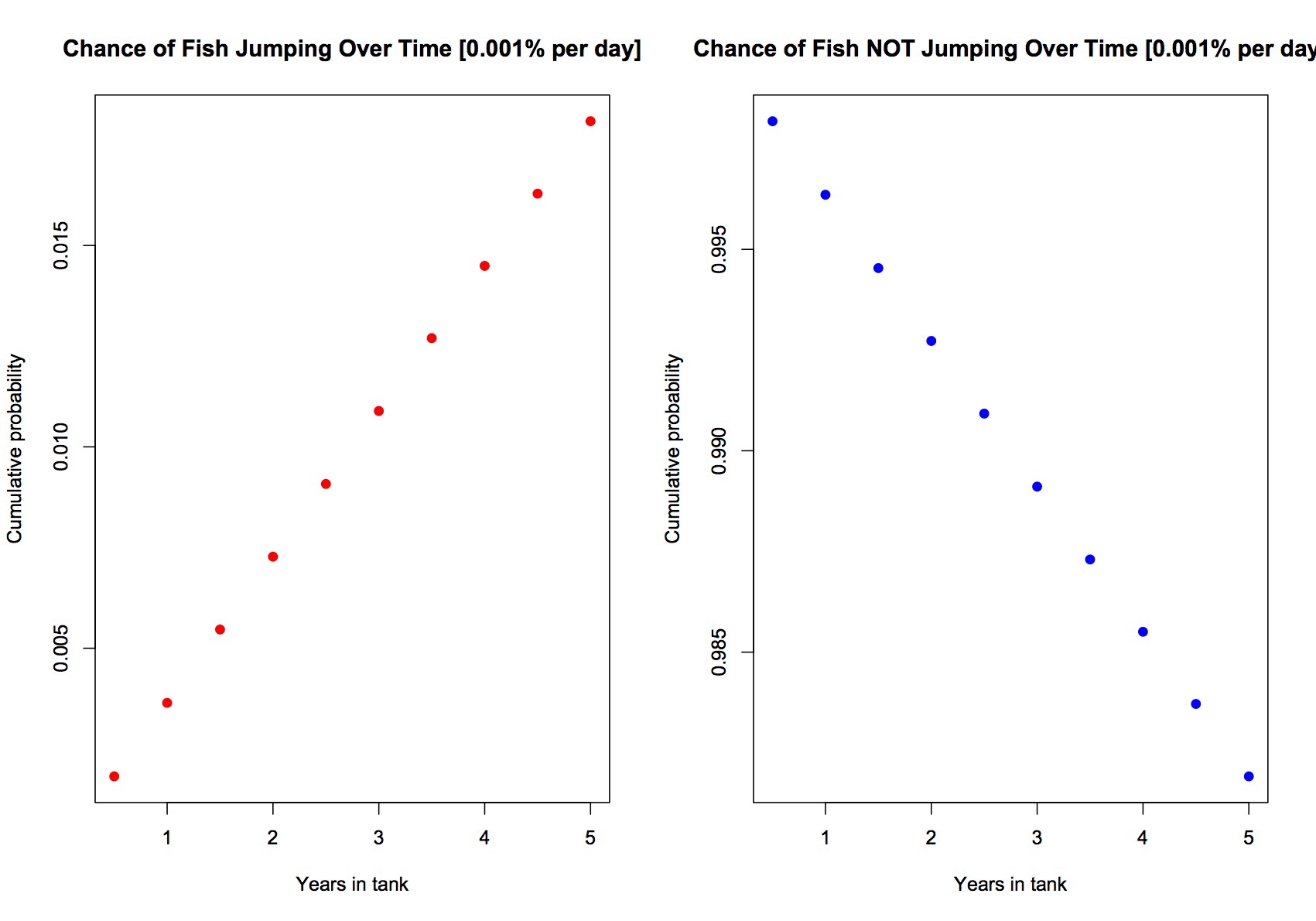
Finally, the last model has daily probability of jumping at 1 in 100,000 (0.001%). This is the safe zone. You can keep this fish in an open top without any significant risk. At 5 years, the probability that this fish went carpet surfing is about 2%... you can take that risk.
While this model is very simple, I think it captures the stochastic nature of fish jumps.
In terms of real-world advice. It is just a matter of knowing the species you plan on keeping, their propensity for jumping, and how much risk you are willing to take with your fish. If you want to guarantee no jumping, then a well fitting / well constructed cover is necessary. For some species, the probability of jumping can be low enough, that it is very conceivable that you can keep them in an open top tank for a long period of time without any incidents... just keep in mind that rare events can and do happen given enough time.
If you are interested in running these simulations, here is some quick r code (r is free, but requires a bit of know how to access)
Just copy and paste this into r to explore different scenarios
dailyp=1/100000 #set this to the daily probablity
par(mfrow=c(1,2)) # initialize plot area
pjump=c() #initialize prob jump array
t=c() # initialize time in years array
for (time in c(0.5,1,1.5,2,2.5,3,3.5,4,4.5,5))
{t=c(t,time)
pjump =c(pjump,1-pbinom(0,size=round(time*365),prob=dailyp))
}
plot(t,pjump,main=c("Chance of Fish Jumping Over Time [",dailyp,"0.001% per day]"),xlab="Years in tank",ylab="Cumulative probability",pch=19,col='red')
plot(t,(1-pjump),main=c("Chance of Fish Jumping Over Time [",dailyp,"0.001% per day]"),xlab="Years in tank",ylab="Cumulative probability",pch=19,col="blue")
Sent from my iPhone using Tapatalk
I thought it would be fun to put this out there after some discussions on the leopard wrasse thread. Essentially; some folks claim that a certain group of fish never jump (because of personal experience of keeping a few fish) while others claim that the same group of fish are jumpers and are thus ultimately doomed to certain death in an open top tank. This little writeup shows how both view points can be reconciled with some simple math.
Ok, we hear a lot of general statements about certain fish being jumpers versus others that are not. But obviously, there are some individual specific tendencies (personality), species specific tendencies, genera specific tendencies, and all of this is modified by the tank environment (etc. size of tank, depth, interactions with other fish). I don't really think that fish are either jumpers or not jumpers... way too binary. For the simplicity of the model developed below, lets think of fish have a 'probability' of jumping for any given day; this probability depends on species (some species of fish/wrasse have higher probabilities of jumping than others) and tank environment / scape. We can probably all agree that most fish can in theory jump, so the probability of jumping is almost always a number that is greater than zero.
If the probability of jumping is greater than zero and substantially high. (say 10% a day), then it is inevitable that the fish will jump given enough time, and that a cover is absolutely needed to keep the fish alive in a tank.
Even if the probability of jumping is really low, say, 1 in 100,000 (0.001%) a day... it doesn't mean that the fish will never jump. Given enough time, rare events will occur (think of people winning the lottery, or getting struck by lighting... it happens, but it is rare). When we are dealing with such low probabilities, then it is totally conceivable to see how some reefers can keep the same species in an open top without them ever jumping, while others having them jump a few times... (just like some people win the lottery while most don't; you can't argue that just because you didn't' win the lottery, that nobody wins the lottery; also, you can't argue that if you win the lottery, than every one will win the lottery)...
So i decided to explore some models of fish jumping in an open top tank given a CONSTANT (assumption) daily probability of jumping. The constant assumption and the discrete nature of jumping (and dying) vs. not jumping (and living) make this problem very easy to model with the binomial distribution. if you were sick during math in high school, then the binomial is the little (n choose k) equation, where you predict the number of success or failures in N trials, assuming the probability of success or failure is constant. You can use the binomial to determine the probability of tossing a fair coin 20 times and getting only 5 tails for example.
In the context of fish jumping, we set the probability of success = daily probability of fish jumping, and ask how many times we observe 0 jumps over time... that gives us the probability of fish NOT jumping... 1- probability of fish NOT jumping is the same as the probability of fish jumping.
So here is the first model "“ assuming a fish has a 1% chance of jumping per day"¦ The probability that this fish would have jumped within the first year is close to 97.5%, The probability of this fish NOT jumping on you for a year is a measly ~2.5%... You NEED to get a cover if you want to keep this fish as the chance of keeping one in a tank with an open top for more than a few months are incredibly LOW.

The second model has a daily probability of jumping at 3 in 10,000 (.03%); here we get into the grey zone. The chances of this fishing jumping by year one is about 10%, year 2 is about 20%, year 3 is about 30%, and year 5 is about 45%. The flip coin of this is you can almost certainly keep this fish alive in an open top tank (i.e. chance of fish NOT jumping) for a year, or two with only a small risk of it jumping). By 5 years though, it gets very dicey "¦ that is to say that half of the people that attempt this fish in an open top tank for 5 years will be successful while the others will not. This is where we tend to see a lot of debate between reefers; One will argue that I kept fish X for 5 years in an open top without it carpet surfing, so "œthey are not jumpers", while another will say, I tried fish X and it went carpet surfing, so "˜they are jumpers"; here is where the fallacy of observation bites us in the *** (with the binomial distribution laughing in the background).

Finally, the last model has daily probability of jumping at 1 in 100,000 (0.001%). This is the safe zone. You can keep this fish in an open top without any significant risk. At 5 years, the probability that this fish went carpet surfing is about 2%... you can take that risk.

While this model is very simple, I think it captures the stochastic nature of fish jumps.
In terms of real-world advice. It is just a matter of knowing the species you plan on keeping, their propensity for jumping, and how much risk you are willing to take with your fish. If you want to guarantee no jumping, then a well fitting / well constructed cover is necessary. For some species, the probability of jumping can be low enough, that it is very conceivable that you can keep them in an open top tank for a long period of time without any incidents... just keep in mind that rare events can and do happen given enough time.
If you are interested in running these simulations, here is some quick r code (r is free, but requires a bit of know how to access)
Just copy and paste this into r to explore different scenarios
dailyp=1/100000 #set this to the daily probablity
par(mfrow=c(1,2)) # initialize plot area
pjump=c() #initialize prob jump array
t=c() # initialize time in years array
for (time in c(0.5,1,1.5,2,2.5,3,3.5,4,4.5,5))
{t=c(t,time)
pjump =c(pjump,1-pbinom(0,size=round(time*365),prob=dailyp))
}
plot(t,pjump,main=c("Chance of Fish Jumping Over Time [",dailyp,"0.001% per day]"),xlab="Years in tank",ylab="Cumulative probability",pch=19,col='red')
plot(t,(1-pjump),main=c("Chance of Fish Jumping Over Time [",dailyp,"0.001% per day]"),xlab="Years in tank",ylab="Cumulative probability",pch=19,col="blue")
Sent from my iPhone using Tapatalk
Last edited:
